Margaret LeMone | 7 January 2010  •  Have you ever looked up in the sky and seen something totally surprising? While walking near our office with my friend Sandra on the early afternoon of 29 December 2009, I pointed out a partial halo around the sun.  The halo’s radius (the distance between the sun and the halo) was 22 degrees, or about the width of your hand if you held it at arm’s length and spread your fingers fully. On the right side of the halo, there was a sundog or “parhelion” —a bright spot at the same height above the horizon as the sun.

Figure 1.  Circumzenithal arc, looking straight up.

These features were interesting enough. But as we began looking more closely at the sky, we noticed something much more unusual straight overhead—an “upside-down rainbow.” This feature, shown in Figure 1 in a photo taken with the camera pointing straight up, is called a circumzenithal arc.  The center (lowermost part) of the arc was directly over the sun.  Note that the red is at the bottom, whereas in a “normal” rainbow, it is at the top. However, in both cases, the red band lies along the outermost edge of the arc.  This photograph was taken at 1:45 p.m. MDT.

The optics show evolved further as we kept watching. About 2:00 p.m., looking toward the other side of the sky, we witnessed a parhelic circle, along with a  sundog-like bright patch in the middle of it (Figure 2, below).

This bright spot is called a “120 degree parhelion” because it lies 120 degrees horizontally from the Sun, or about one-third the way around the horizon. In contrast, the “normal” parhelion, or sundog, lies only 22 degrees from the sun horizontally.  For example, if the Sun had been south-southwest of us (at about 200 degrees on a compass), the bright spot of this 120-degree parhelion would have been at (200 + 120) = 320 degrees, or roughly northwest of us. The more common 22-degree parhelion would have been at (200 + 22) = 222 degrees, or roughly southwest of us.

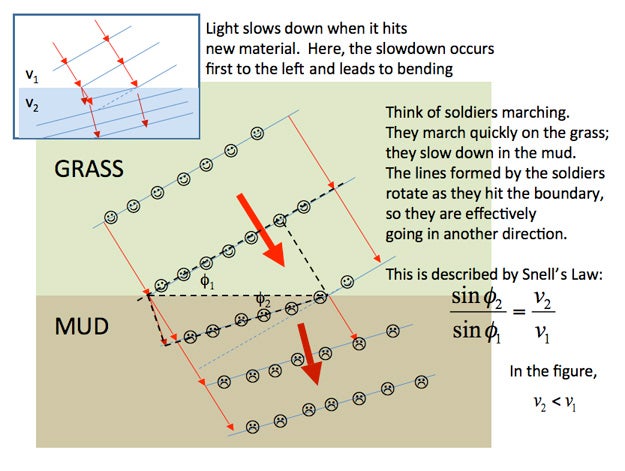
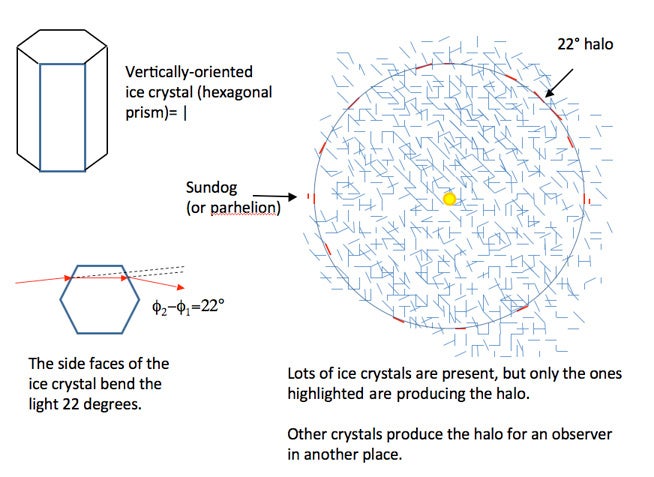
What causes these arcs and sundogs?  We associate such displays with cloud made up of ice crystals (cirrus, in this case) that serves as prisms.  Light rays from the sun are bent upon entering and leaving the crystal; this is called refraction.  The new direction of the sun’s rays upon leaving the crystals is determined by the differences in the composition of air and ice and the angle of the faces through which the rays enter and leave the crystal.  Light rays can also be reflected by the ice crystals.  When you see refracted or reflected light, it is often coming from a different direction than the location of its source.  For the 22-degree halo, for example, the light that you see was originally directed 22 degrees away from you as it left the Sun. The light rays were then bent 22 degrees by the crystal—i.e., back toward you (see "Optics 101" at the end of this blog for a diagram).

Figure 2.  Parhelic circle and 120-degree parhelion, looking northwest at 2:00 p.m. MST.  The parhelic circle is the subtle arc just above the middle of the picture; the 120-degree parhelion on the circle just to the right of the center of the picture.

For the 22-degree halo and for a typical sundog, the light enters one face of a hexagonal crystal and exits at another face angled at 60 degrees to the first face.  (If the faces were exactly parallel, the light ray would bend twice, but end up going in the same direction.)  Although this refraction is taking place in ice crystals throughout the cloud, we see only the light coming through those crystals that are located about 22 degrees from the Sun.   Near-vertical crystals contribute to the sides of the halo, and near-horizontal crystals contribute to its top and bottom, with crystals at other orientations contributing to the rest of the halo.  Similarly, light coming from the vertical crystals forms the sundogs, which are often seen on both sides of the sun.

Because different wavelengths of light are bent at slightly different angles, there is a slight color separation.  The light-ray paths for sundogs (parhelia) are similar, with the sides of the ice crystal vertical.  Because red light rays are not bent as much as light of shorter wavelengths, the side of a sundog nearer the sun is the redder one.

Wider and wider

What about the parhelic circle, which extends much farther from the Sun than the halos and sundogs discussed above?  When light rays reflect off the inside of an ice crystal two or more times, the extra reflections mean that we see the light from crystals located 120 degrees away the Sun.

The parhelic circle is caused by reflection off vertical ice-crystal faces (external reflection). Internal reflections (the light entering the ice crystal and reflecting off a crystal face from the inside) also contribute. For the circumzenithal arc, the light enters the top of a prism whose side faces are perpendicular to the faces at the top and bottom, and exits out a side.  Again, the red light bends less than the shorter wavelengths, so the red is closer to the sun.

Wikipedia, the website Atmospheric Optics, and the UCAR-based Windows to the Universe site will give you a great deal more information on these and other optical phenomena.  With a little bit of background, you can learn to appreciate the mathematics and physics behind these features as well as their sheer beauty.

Optics 101:  Refraction and ice crystals

Below are two mini-tutorials I put together to accompany this post. The first one uses a battlefield analogy to show how a light ray gets bent, or refracted, as it enters a prism. (You don't need to follow the mathematics to understand the analogy!) The second one shows how only a few of the ice crystals in a cloud are oriented in such a way as to produce a halo.

See all News